“数学中国”公众号文章《数学家如何做到“十赌十赢”?》解决了我一直以来对“赔率”定义的疑问：在关于“轮盘赌”游戏的描述中，我明白如果下注金额为m，赢一把净赚nm（下注金额m也一并返还），则赔率为n。

文中还科普了“凯利公式”，我用自己的话通俗演绎出来就是：（不妨设每次下注金额为1），单次下注平均赢钱金额，占单次赌赢赢钱金额的比例，应为单次下注金额占总资金额度的比例。同时可以注意到，在单次赌局平均赢钱金额不变的情况下，胜率越大，赔率越小，反之则反。上网进一步做功课，可知这是二元结果赌局下的凯利公式特殊形式，但已然很能指导人的决策了。

直观理解“凯利公式”，可以作如下设想。例如单次胜率为1/100，赔率为99，则单次下注赢钱金额期望为0，故单次下注金额也应为0，也就是说这种赌局没必要参加。当单次赌局赢钱金额期望值为正时，可以加入赌局，并且，单位赌资单次赌局平均赢钱金额占赔率的比例越大，下注金额占总资金的比例也应越大。极端情况下，单次赌局单位赌资平均赢钱金额与赔率一致，说明这是必赢之局，应该all in。

我把凯利公式写成更直观的形式：单次下注资金比例=单次获胜概率-单次失败概率/单次赌赢赢钱倍率（赔率），也即下注比例=胜率-败率/赔率=胜率-(1/赔率-胜率/赔率)=胜率(1+1/赔率)-1/赔率。（发现展开后也没更直观，我直接说好了：）遇到胜率大赔率大的事情，要多多投入资源乃至all in；遇到胜率小赔率小的事情，要尽量躲开。

以上都还好理解，但世间之难往往是遇到胜率大赔率小或胜率小赔率大的事情，要正确估计投入分配比例。这其间的关键在于如何准确评估胜率与赔率大小。有的人终其一生过于求稳，尽管保住了胜率，但却困于过低的赔率，终是多有抱憾；有的人在高赔率诱惑下动辄梭哈冒进，对自身全部资本实力认识不足，不知道有多大本钱办多大事，很容易招致风险失控。

江南愤青陈宇有篇热文《概率和赔率的一些实践思考》，认为信贷业务是一种不好的商业模式。我理解其含义是，借钱经常是不划算的赌局——资金融出方以借款本金下注，赌的是资金融入方按期还本，并赔以利息。尽管其胜率很大，但赔率太小（仅有利率加成），因此一般被认为是不划算的赌局。所以，资金借出方要么是资本雄厚（所以下注金额不过自身九牛一毛），要么以“砍头息”提高赔率，方能维持赌局。但其实民间借贷中，连正的平均赢钱金额期望都没有（例如约定不求利息回报），则一般是在赔率中注入了人情关系收益加成，方才能将此本应避而远之的赌局进行下去。

同样可以分析人生在世一些稳赚不赔或稳赔不赚的买卖。例如高考应试阶段的努力，以考“双一流”为例，备考者以时间精力成本下注，胜率或许不大，但赔率极大（我知道有人可能会拿名校学历不如学区房来说事，但须知备考的赌注不过是相较报考一般院校多付出的努力，假设填志愿环节没有随机性因素）。又如完美主义或曰“强迫症”，此类病患以异乎寻常的时间与专注下注，胜率极大，但赔率极低，不过是对差错损失的一点点降低，绝对是一个需要远远避开的必输之局。

再者，凯利公式中的胜率、赔率皆为统计上有意义，也即需要足够多次的重复试验方能让大数定律发挥作用，因此要取得终胜，往往需要反复多次的下注参与，这也是坚持不懈、连续创业等事有竟成者背后的逻辑。

还看过一个不那么好的例子，就是为什么一些官员老板信迷信。这类人一般愿意不断尝试低胜率高赔率的事情，每次下注较自身实力而言相对有限（精力与财力投入等），但架不住胜率其实没那么低而赔率有时确实高，同时他们往往热衷于持之以恒的钻营经营，仿佛这种实践能得到类似打游戏的即时奖励反馈。这类人发迹的不二法门就是不停地在（相对）低胜率同时高赔率的事物上下注，余下的就交（迷）给（信）上天好了。

从某种意义上说，人生在世，凡事有所成，皆认知的变现。而人对万事万物的认知，抽象到凯利公式上，就是对胜率与赔率的认知。

当然，我并没有继续深入探求凯利公式的是如何推导而来（卡在了随机过程数学期望求解上），只是就事论事对其应用进行了一番思考，人的一生就是一个不断试错的随机过程，简洁公式蕴含的深刻道理，数学之美诚不我欺。

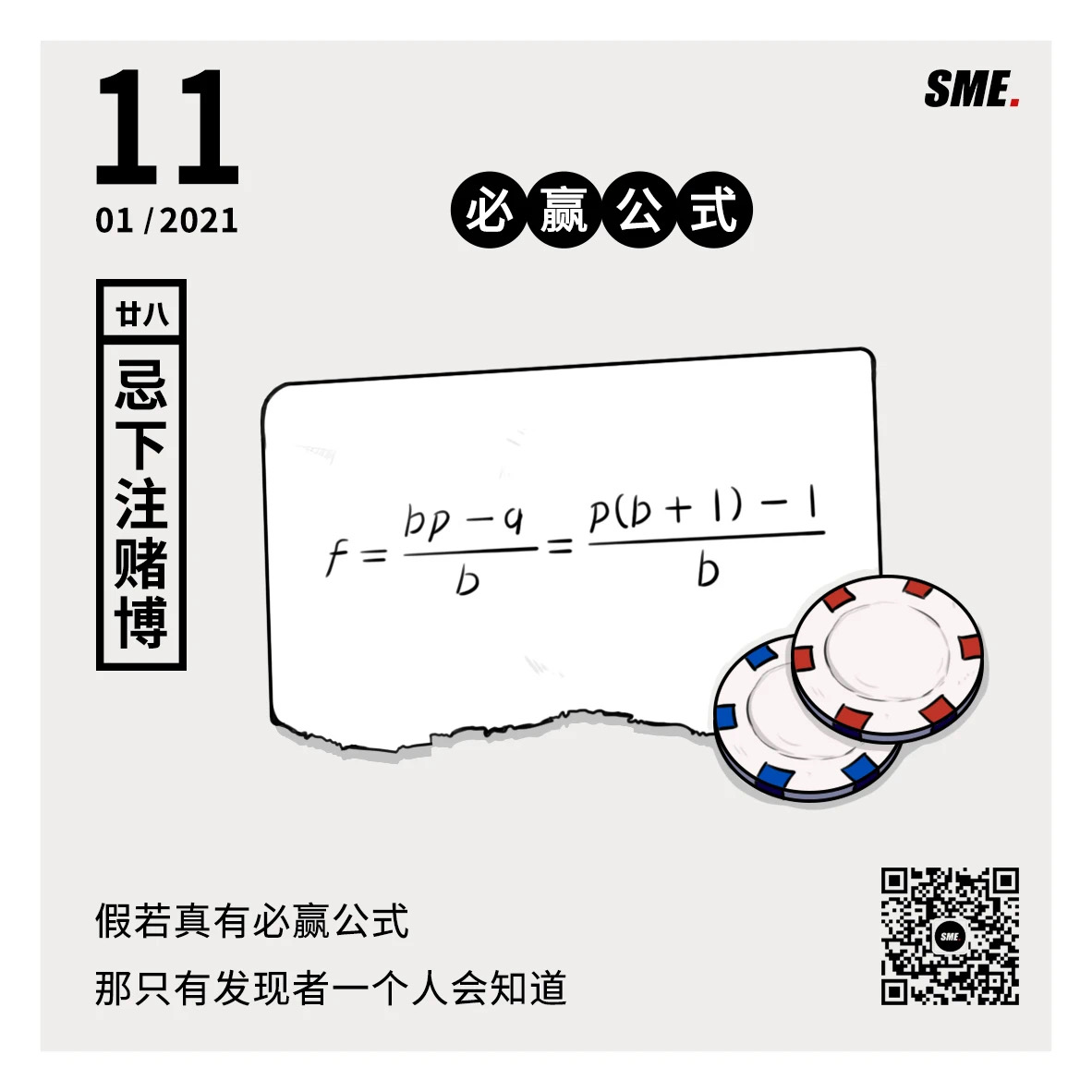
最后盗用公众号“SME科技故事”的一张图作为结尾（侵删）。