各参数与具体情形如图所示,图中蓝色线段代表刚性直棍,以外墙角壁为纵横轴建立平面直角坐标系,内墙角为C点。要求刚性直棍能横转过墙角时长度L的最大值。
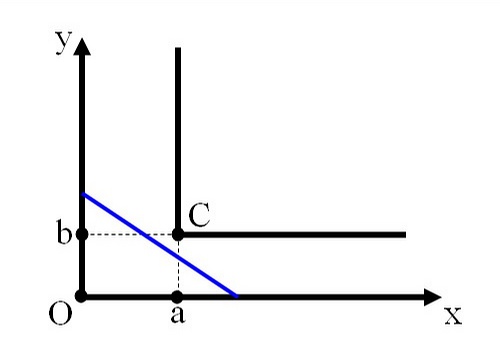
这是我某次高三月考数学试卷的压轴题,(当时整体的进度应该是刚复习到三角函数那个部分,)老师讲评试卷时给出的答案里是用三角函数结合导数求极值做出来的。我多有不解。因为考察那种解答,我感觉即便在b无限趋向于0时,直棍在横转过墙角时似乎也不会受到必然的阻碍。
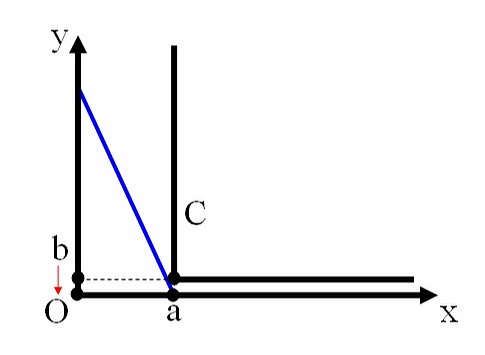
当时在考场上,我的想法是:保持直棍的两端分别紧贴两面墙,然后让直棍连续转动,求出其轨迹的包络线(以L为参数);当包络线与墙角C相切时,L即取得最大值。但我认为求这样的包络线要用到高深的数学方法,由是知难而退。
试卷讲评时我把这一想法跟坐我左边的彭兄说,他不置可否。
后来我自学《西方经济学(微观部分)第四版》P172图5-10“最优生产规模的选择和长期总成本曲线”时,觉得包络线的实质就是“求每一横坐标下最低的纵坐标”。我似乎受到什么启发,又想起了“刚性直棍横过墙角”这道题。
我根据“直棍长度恒为L,且直棍的两端始终保持分别紧贴着两面墙壁”可列出直棍所在直线的方程:(其中k为斜率)
$$y=kx-\frac{kL}{\sqrt{1+k^2}}$$
设刚性直棍横转过墙角的初态为
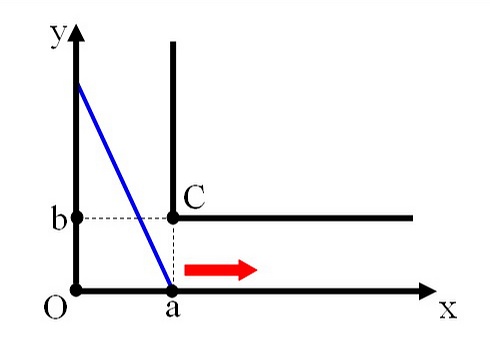
对应于\(k=-\frac{\sqrt{L^2-a^2}}{a}\)
终态(完全通过)为(对应于k=0)
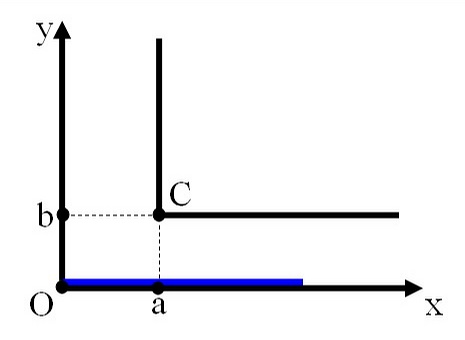
则直棍横过墙角的过程,就是k从\(-\frac{L^2-a^2}{a}\)连续增大到0的过程。
可见直棍能横过墙角的一个充分条件就是,当k从\(-\frac{L^2-a^2}{a}\)向0增大时,直棍所在直线在横坐标a处所对应的纵坐标\(y_a=ka-\frac{kL}{\sqrt{1+k^2}}\)始终小于b.
当L取定时,将其对k求导并令其等于0:\(\frac{\mathrm{d}y_a}{\mathrm{d}k}=a-\frac{L}{(1+k^2)^\frac{3}{2}}=0\)
可知:对于每一个确定的L,横坐标a处对应的纵坐标始终在\(k=\sqrt{(\frac{L}{a})^\frac{2}{3}-1}\)时取最大值\(y_{a(max)}=(L^\frac{2}{3}-a^\frac{2}{3})^\frac{3}{2}\).而这是随L单调递增的函数。
令其等于b,可得符合题意要求的L的最大值为:
$$L_{max}=(a^\frac{2}{3}+b^\frac{2}{3})^\frac{3}{2}$$
这个结果与当年老师给出的答案是一致的。
进一步地,我想求出长为L的刚性直棍很过墙角,保持两端分别紧贴两面墙时的包络线。
包络线的定义域为:\([0,L]\).取定\(x_0\)(L显然也是早已被取定的),求\(x=x_0\)处最大的y,即\(y_0\).
考虑长为L的直棍所在直线的方程
$$y=kx-\frac{kL}{\sqrt{1+k^2}}$$
在每一个确定的\(x_0\)处,纵坐标y的值都唯一地由斜率k的值确定。
对k求导并令导数为0:
$$\frac{\mathrm{d}y_0}{\mathrm{d}k}=x_0-\frac{L}{(1+k^2)^\frac{3}{2}}=0$$
解得k取\(-\sqrt{\left(\frac{L}{x_0}\right)^\frac{2}{3}-1}\)时y最大:\(y_{0(max)}=\left(L^\frac{2}{3}-x_0^\frac{2}{3}\right)^\frac{3}{2}\).
所以包络线的方程为:
$$y=\left(L^\frac{2}{3}-x^\frac{2}{3}\right)^\frac{3}{2}$$
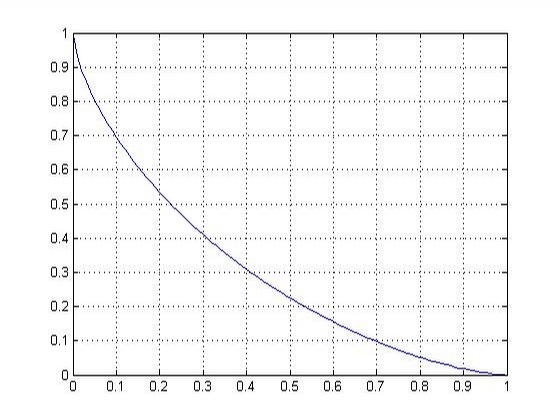
或写成更为漂亮的形式:
$$x^\frac{2}{3}+y^\frac{2}{3}=L^\frac{2}{3}$$
当刚性直棍横过墙角时,棍体一定全部都在包络线与纵、横轴所围成的范围内运行。另一方面,棍体也会遍历包络线上的每一点。即对棍体来说,包络线上的任何点都不能被覆盖从而变得不可及。对于内墙角C来说,包络线以内的任何点都是不可及的。